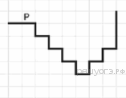
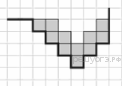
Циклические алгоритмы
Очень часто при составлении алгоритмов некоторую последовательность команд приходится выполнять многократно. Для решения таких задач применяют циклический алгоритм.
В языке КуМир есть специальные команды для организации программы с циклическим алгоритмом.
Существует три основных типа команд, с помощью которых можно реализовать циклы в алгоритмах. В КуМире они называются команды повторения.
| Цикл n раз | Цикл пока | Цикл «до тех пор» |
| Общий вид команды:
нц тело_цикла кц |
Общий вид цикла пока: нц пока условие · тело_цикла кц
|
Общий вид цикла до тех пор: нц · тело_цикла кц_при условие |
| Команды тела цикла будут выполнены n раз. |
При выполнении цикла пока Робот циклически повторяет следующие действия: · Проверяет записанное после служебного слова пока условие. · Если условие не соблюдается, то выполнение цикла завершается и Робот начинает выполнять команды, записанные после кц. |
При выполнении цикла до тех пор Робот циклически повторяет следующие действия: · Выполняет тело цикла. · Проверяет записанное после служебного слова кц_при условие. ∙ Если условие соблюдается, то выполнение цикла завершается и Робот начинает выполнять команды, записанные после кц_при. Если же условие не соблюдается, то Робот выполняет тело цикла, снова проверяет условие и т.д. |
Цикл n раз
Видео: Урок 3. КуМир. Цикл со счетчиком, автор A Ch
Цикл пока
Видео: Урок 2. КуМир. Цикл с условием, автор A Ch
Задание 1.